A. Ukuran Sudut
1. Ukuran Derajat
Besar sudut dalam satu putaran adalah 360°. Berarti 1°= 1/360 putaran. Ukuran sudut yang lebih kecil dari derajat adalah menit ( ‘ ) dan detik ( “ ).
Hubungan ukuran sudut menit, detik, dan derajat adalah:
2. Ukuran Radian
Satu radian adalah besar sudut pusat busur lingkaran yang panjangnya sama dengan jari-jari.
3. Hubungan Derajat dengan Radian
Untuk mengubah sudut sebesar 𝛉 ke dalam satuan radian, menggunakan rumus:
Dan untuk mengubah sudut sebesar X radian ke dalam satuan derajat, menggunakan rumus:
Contoh Soal
1. Nyatakan sudut 0,65 radian dalam satuan derajat!
Jawab :
2. Nyatakan sudut 154° ke satuan radian!
Jawab:
3. Suatu lingkaran memiliki panjang busur 15 cm dan dengan sudut pusat 45°, carilah jari-jari lingkaran tersebut!
Jawab:
Kita harus merubah 𝛉= 45° ke dalam bentuk radian.
B. Perbandingan Trigonometri pada Segitiga Siku-Siku
Perhatikanlah gambar berikut!
Jika dipandang dari sudut 𝛉, maka sisi BC disebut sisi depan, sisi AB disebut sisi samping, dan sisi AC disebut sisi miring.
Jika sisi AB = x, sisi BC = y, dan sisi AC = r, maka
Contoh soal
1. Perhatikan gambar berikut!
Diketahui panjang AC = 9 cm, dan panjang AB = 12 cm, dengan sudut b = 𝛉. Tentukan nilai dari sin 𝛉, cos 𝛉, dan tan 𝛉!
Pemecahan:
2. Jika sin 15°= y. Tentukan nilai trigonometri berikut dalam y!
a. Cos 15°
b. Tan 15°
c. Sin 75°
d. Cos 75°
e. Tan 75°
f. Cosec 15°
g. Cotan 75°
h. Sec 75°
Pemecahan:
a. Cos 15°
b. Tan 15°
c. Sin 75°
d. Cos 75°
e. Tan 75°
f. Cosec 15°
g. Cotan 75°
h. Sec 75°
3. Jawablah pertanyaan berikut!
b. Tentukan nilai dari
Pemecahan:
b. Nilainya adalah
C. Perbandingan Trigonometri Sudut Berelasi
Dalam satu putaran, yaitu 360°, sudut dibagi menjadi empat relasi, yaitu:
1. Kuadran I : 0°≤ α ≤ 90°
2. Kuadran II : 90° < α ≤ 180°
3. Kuanran III : 180° < α ≤ 270°
4. Kuadran IV : 270° < α ≤ 360°
Perhatikan gambar berikut!
1. Perbandingan Trigonometri Sudut di Kuadran I
Pada ∆ AOC, berlaku:
Pada ∆ BOC, berlaku:
2. Perbandingan Trigonometri Pada Sudut Kuadran II
Pada ∆ AOC, berlaku: ∠α = 180°- 𝛉
3. Perbandingan Trigonometri Pada Sudut Kuadran III
Pada ∆ AOC berlaku: ∠ AOP = α
4. Perbandingan Trigonometri Pada Sudut Kadran IV
sin (360° - 𝞪) = - sin 𝞪
cos (360° - 𝞪) = cos 𝞪
tan (360° - 𝞪) = - tan 𝞪
cosec (360° - 𝞪) = - cosec 𝞪
sec (360° - 𝞪) = sec 𝞪
cotan (360° - 𝞪) = - cotan 𝞪
5. Perbandingan Trigonometri Untuk Sudut Diatas 360° atau Sudut Negatif
a. Perbandingan Trigonometri Untuk Sudut Diatas 360°
Sin (k × 360° + 𝞪) = sin 𝞪
Cos (k × 360° + 𝞪) = cos 𝞪
tan (k × 360° + 𝞪) = tan 𝞪
cosec (k × 360° + 𝞪) = cosec 𝞪
sec (k × 360° + 𝞪) = sec 𝞪
cotan (k × 360° + 𝞪) = cotan 𝞪
Keterangan:
k = banyaknya putaran, dengan nilai k adalah bilangan bulat positif.
b. Perbandingan Trigonometri Sudut Negatif
Sin (- 𝞪) = -sin 𝞪
Cos (-𝞪) = cos 𝞪
tan (-𝞪) = -tan 𝞪
cosec (-𝞪) = -cosec 𝞪
sec (-𝞪) = sec 𝞪
cotan (-𝞪) = -cotan 𝞪
Contoh Soal
1. Nyatakan sudut berikut kedalam perbandingan trigonometri sudut lancip positif!
a. Sin 175°
b. Cos 325°
c. Sec (-225°)
d. Tan 780°
e. Sin 3500°
2. Diketahui sin 35° = 2k, nyatakan trigonometri sudut berikut dalam k!
a. Sin 55°
b. Cos (-215°)
c. Tan 125°
d. Cosec 935°
e. Sin 665°
Pemecahan:
D. Persamaan Trigonometri sin x = sin α, cos x = cos α, dan tan x = tan α
1. Jika sin x = sin α, maka x = α + k . 360° atau x = (180° - α) + k . 360°
2. Jika cos x = sin α, maka x = α + k . 360° atau x = (360° - α) + k . 360° = -α + k . 360°
3. Jika tan x = tan α, maka x = α + k . 180°
Contoh Soal
1. Tentukan himpunan penyelesaian dari persamaan trigonometri berikut!
a. Sin x = sin ⅚ 𝛑, 0 ≤ x ≤ 2𝛑
b. Tan x = tan ⅓𝛑, 0 ≤ x ≤ 2𝛑
c. Cos x = cos 150°, 0° ≤ x ≤ 360°
Pemecahan:
a. Sin x = sin ⅚ 𝛑, 0 ≤ x ≤ 2𝛑
Himpunan penyelesaian = {⅚ ,⅙𝛑}
b. Tan x = tan ⅓𝛑, 0 ≤ x ≤ 2𝛑
Himpunan penyelesaian={⅓𝛑 ,4/3 𝛑}
c. Cos x = cos 150°, 0° ≤ x ≤ 360°
Himpunan penyelesaian= {150°,210°}
2. Tentukan himpunan penyelesaian dari persamaan trigonometri berikut!
a. Sin x = cos 300°, 15°≤ x ≤ 360°
b. Cos x = cotan 135°, 0°≤ x ≤ 360°
c. Tan x = sin 0°, 180°≤ x ≤ 360°
d. Cos 3x = cos 180°, 0° ≤ x ≤ 360°
e. Sin (30°+x) = sin 75°, 0°≤ x ≤ 270°
f. Sin (4x+38°) = sin 173°, 0° ≤ x ≤ 360°
g. Tan x = ⅓√3, 0 ≤ x ≤ 2𝛑
Pemecahan:
a. Sin x = cos 300°, 15°≤ x ≤ 360°
Himpunan penyelesaian={30°,150°}
b. Cos x = cotan 135°, 0°≤ x ≤ 360°
Himpunan penyelesainnya adalah {180°}
c. Tan x = sin 0°, 180°≤ x ≤ 360°
Himpunan penyelesaian= {180°,360°}
d. Cos 3x = cos 180°, 0° ≤ x ≤ 360°
Himpunan penyelesain={60°,180°, 300°}
e. Sin (30°+x) = sin 75°, 0°≤ x ≤ 270°
Himpunan penyelesain={45°,75°}
f. Sin (4x+38°) = sin 173°, 0° ≤ x ≤ 360°
Himpunan penyelesaian={33,75°; 82,25°; 123,75°; 172,25°; 213,75°; 262,25°; 303,75°; 352,25°}
g. Tan x = ⅓ √3, 0 ≤ x ≤ 2𝛑
Himpunan penyelesaian = {⅙𝜋, 7/6 𝜋}
E. Identitas Trigonometri
1. Rumus Dasar
2. Menentukan Identitas Trigonometri
a. Ubah bentuk ruas kiri hingga sama dengan bentuk ruas kanan.
b. Ubah bentuk ruas kanan hingga sama dengan bentuk tuas kiri.
c. Kedua ruas diubah hingga didapat bentuk baru yang sama.
Contoh Soal
1. Buktikan bahwa sec2 𝞪 + tan2 𝞪 = 2tan2𝞪+1
2. Buktikan bahwa sec Y – cos Y = sin Y . tan Y
Penyelesaian:
1. sec2 𝞪 + tan2 𝞪 = 2tan2𝞪+1
Ruas kiri
= tan2 𝞪 + 1 + tan2 𝞪
= 2 tan2 𝞪+1
2. sec Y – cos Y = sin Y . tan Y
bukti dengan mengubah ruas kiri
F. Trigonometri Pada Segitiga Sembarang
1. Aturan Sinus
Rumus:
Contoh soal
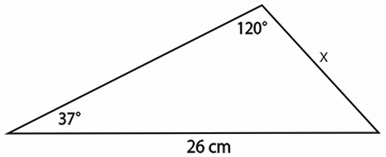
1) Perhatikan gambar berikut!
Tentukan panjang x dalam cm!
Penyelesaian:
2. Aturan Cosinus
Rumus:
a2 = b2+c2 - 2bc cos 𝞪
b2 = a2+c2 - 2ac cos 𝞫
c2 = a2+b2 - 2ab cos 𝞬
Contoh soal
1) Perhatikan gambar berikut!
Tentukan panjang PR!
Pemecahan:
PR2 = RQ2 + PQ2 – 2RQPQ cos ∠ Q
PR2 = 172 + 302 – 2 . 17 . 30 cos 53°
PR2 = 289 + 900 – 1020 . ⅗
PR2 = 1189 – 612
PR2 = 577
PR = √577 = 24,02 cm
3. Luas Segitiga
Rumus:
L = ½ ab sin 𝞬
L = ½ bc sin 𝞪
L = ½ ac sin 𝞫
Contoh Soal
1. Hitunglah luas ABCD berikut!
Pemecahan:
a. Untuk ∆ BCD
Luas ∆ BCD = ½ BD.CD. sin ∠ D
Luas ∆ BCD = ½ . 18√2 . 12√6 . sin 30°
Luas ∆ BCD = ½ . 18√2 . 12√6 . ½ = ¼ . 216√12 = 108√3 cm2
b. Untuk ∆ ABD
Luas ∆ ABD = ½ AD.BD. sin ∠D
Luas ∆ ABD = ½ . 18. 18√2 . sin 105°
c. Luas ABCD
Luas ABCD = Luas ∆ BCD + Luas ∆ ABD
Luas ABCD = 108√3 cm2 + 81√3 + 81 cm2
Luas ABCD = 189√3 cm2 + 81 cm2
Luas ABCD = 327,35 + 81
Luas ABCD = 408,35 cm2




































































No comments:
Post a Comment